
Colorimetría
Los gráficos de tipo mapa de calor, tabular y análisis de brecha utilizan una gama de colores para representar el comportamiento de tus resultados respecto al punto de comparación que seleccionaste en los filtros, por ejemplo respecto a tu resultado del año anterior o a los resultados de las 50 Mejores Empresas Para Trabajar.
COMPARADOR SELECCIONADO

COLOR ROJO
Resultados que tienen una calificación MENOR que la media del punto de comparación.
Mientras más bajo sea con respecto al punto de comparación, el tono del rojo será más intenso.
COLOR GRIS O NEUTRO
Resultados que tienen una calificación IGUAL a la media del punto de comparación.
COLOR VERDE
Resultados que tienen una calificación MAYOR que la media del punto de comparación.
Mientras más alto sea con respecto al punto de comparación, el tono del verde será más intenso.

Significado de la desviación estándar.
Cuando se tienen 60 reactivos en el Trust Index®, cada uno con su resultado específico, es posible calcular el promedo de estos 60 números. Ese promedio es el resultado total del Trust Index® y en estadísticas se le denota con una letra griega μ (“mu”). Si el comparador es este promedio, se pinta de color gris porque representa justo el punto medio de la distribución de los 60 números.
Se puede graficar una distribución de esos 60 resultados, y su representación gráfica podría ser algo parecido a esto:
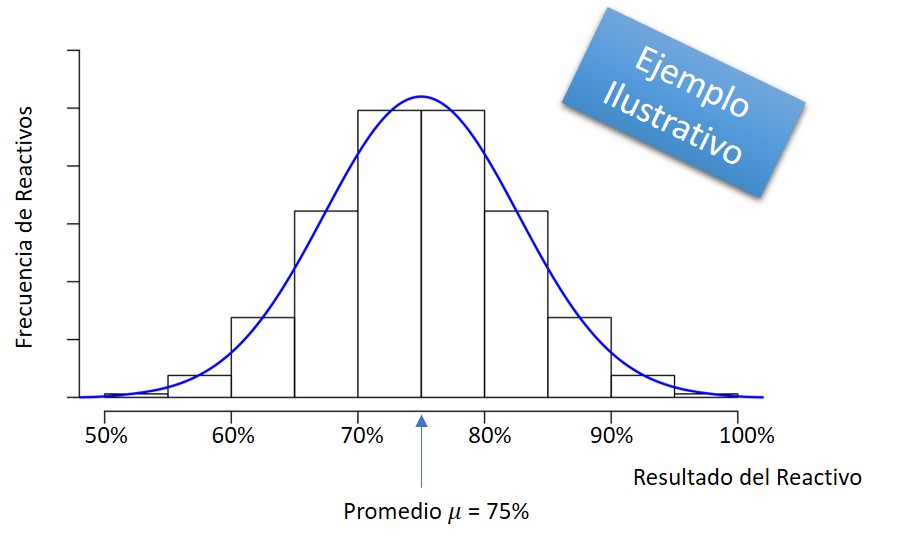
Un gran número de reactivos se concentran justo alrededor del promedio, y serán pocos reactivos los que muestran resultados muy superiores al promedio así como pocos reactivos que muestran resultados muy inferiores al prmedio. La distribución se asemeja a una curva normal o campana de Gauss.
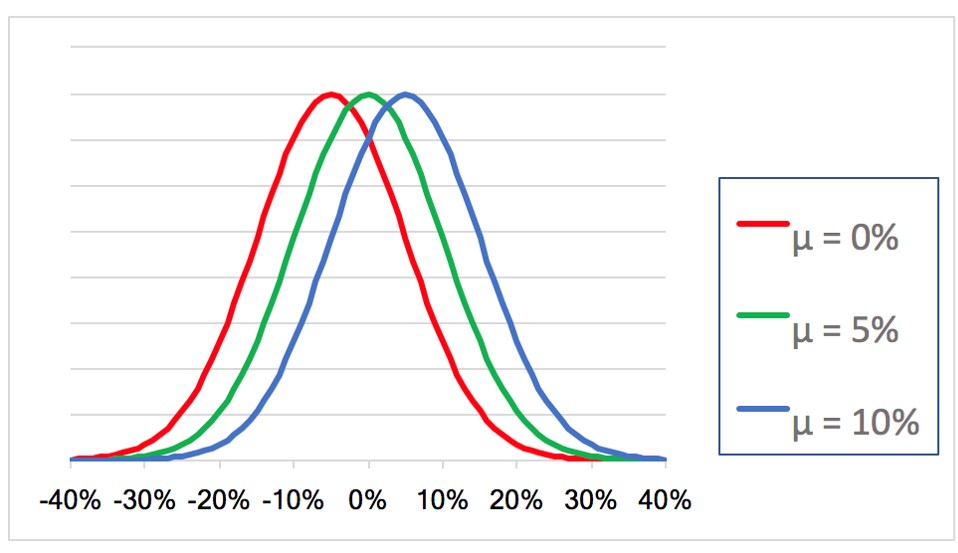
Organizaciones diferentes podrán tener promedios del Trust Index diferentes, con lo cual cada una podrá tener su propia campana de Gauss, con μ´s diferentes.
En el siguiente ejemplo, se muestran 3 campanas de Gauss, cada una con una μ diferente. La de color azul presenta la μ más alta de los tres, mientras que la de color rojo presenta la μ más baja.
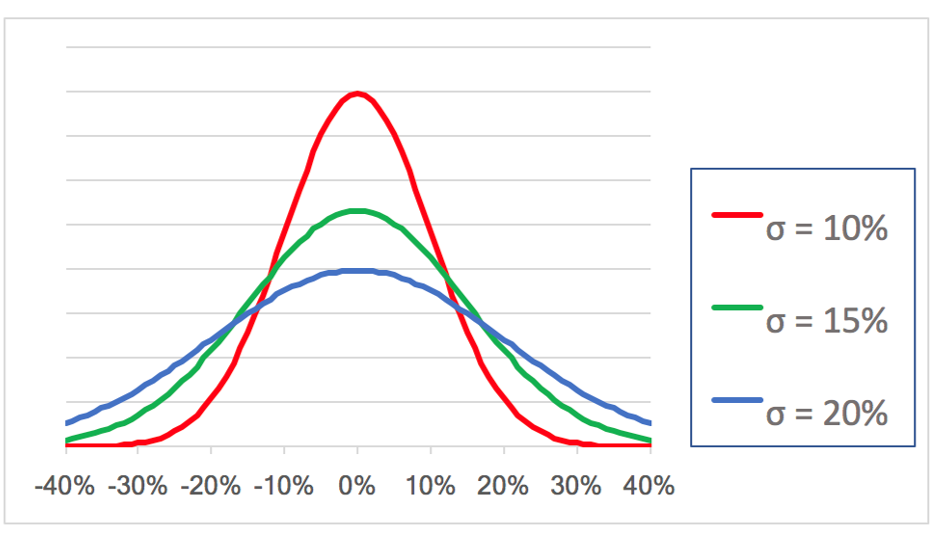
Otra característica importante de las curvas normales son su “grosor”. Algunas presentan un grosor mayor, y otras un grosor menor. En el siguiente ejemplo, se muestran 3 curvas normales con grosores diferentes. La de color rojo presenta el de menor grosor, mientras que la de color azul presenta el de mayor grosor.
Este grosor tiene un nombre, desviación estándar, y se le denota con la letra griega σ “sigma”. Cuando la desviación estándar σ es pequeña, la mayoría de los resultados se concentran “cerca” de su promedio μ y es por ello que la campana se muestra angosta y alta alrededor de μ. Y cuando la desviación estándar σ es grande, la mayoría de los resultados se concentran “lejos” de su promedio μ y es por ello que la campana se muestra muy ancha y chata alrededor de μ.